Question de votre camarade :
"Je rencontre des difficultés face au calcul du TMS à l'aide d'une fonction d'utilité. En effet je ne sais plus comment m'y prendre. Auriez vous le temps de m'expliquer son calcul ?"
Lorsqu'on se déplace le long d'une courbe d'indifférence la perte d'utilité liée à la consommation d'une unité en moins d'un bien doit être exactement compensée par le gain d'utilité lié à la consommation d'une unité supplémentaire de l'autre bien (puisque l'utilité est constante le long d'une même courbe d'indifférence). On a donc :
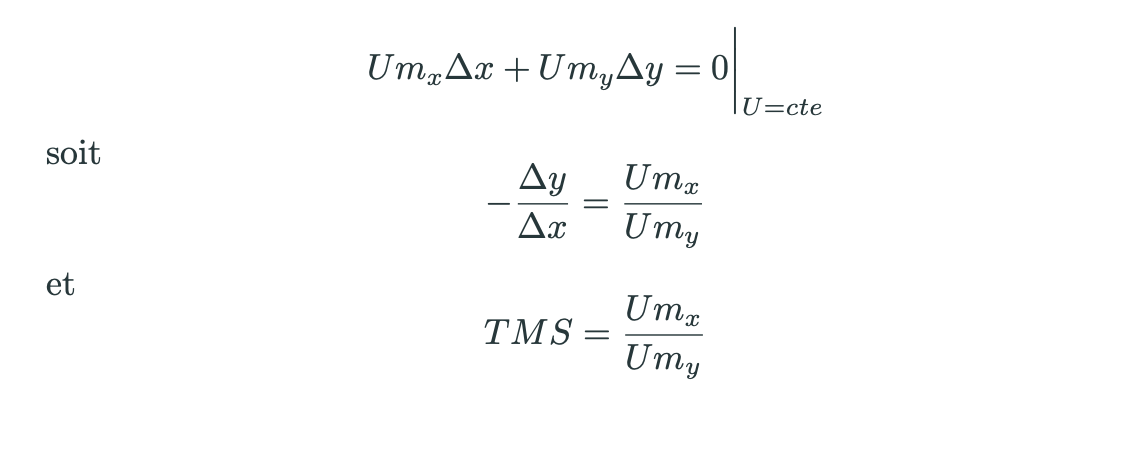
Ici la première equation vous dit que le gain d'utilité lié à l'augmentation de la consommation de X (je consomme delta X unités supplémentaires) multiplié par l'utilité que me rapporte chacune de ces quantités de X supplémentaires est exactement égal à la perte d'utilité liée à la diminution de la consommation de Y (je consomme delta Y unités en moins) multiplié par l'utilité que me rapportait chacune de ces quantités de Y.
En réarrangeant les termes de cette equation on peut montrer que le TMS est donc égal au rapport des utilités marginales. Vous avez un exemple de calcul du TMS à partir de la fonction d’utilité dans l’exercice avec Yaël que nous avons fait en cours ou dans l’exercice supplémentaire en ligne avec Forest Gump.
Bien cordialement,
Valette Jérôme.