Bonjour, je ne comprends pas pourquoi a la question 26 du QCM , le résutat est le panier (6,6) préféré a A(8,2) et B(4,10) lorsqu'on nous demande "Si un consommateur est indifférent entre deux paniers : A = (8, 2) et B = (4, 10), alors la convexité des préférences implique que ce consommateur". En effet j'ai refais le calcul de convexité en prenant la formule:(λx+(1-λ)y) avec λ=0.5. Je trouve le panier ( 5,7).
Bonjour Juliette,
Pouvez vous remettre l'énoncé complet de la question? Les questions sont proposées à chaque fois dans un ordre aléatoire donc le numéro de nous donne aucune indication.
Merci,
Marie Boltz
« si un consommateur est indifférent entre deux paniers : A(8,2) et B(4,10) , alors la convexité des préférences implique que ce consommateur:
a. Prefere A à B
b. Prefere E=(1,20) à A ou B
c. Prefere D=(6,6) à A ou B
d.prefere A à C=(4,4) »
> réponse a. est contradictoire par rapport à l'énoncé
> réponse b. la convexité des préférences ne permet pas de répondre car dans E : il y a une seule unité de bien 1 et dans les paniers A et B il y en a toujours strictement plus que 1.
> réponse d. est impossible par la monotonie des préférences: C est strictement dominé par B.
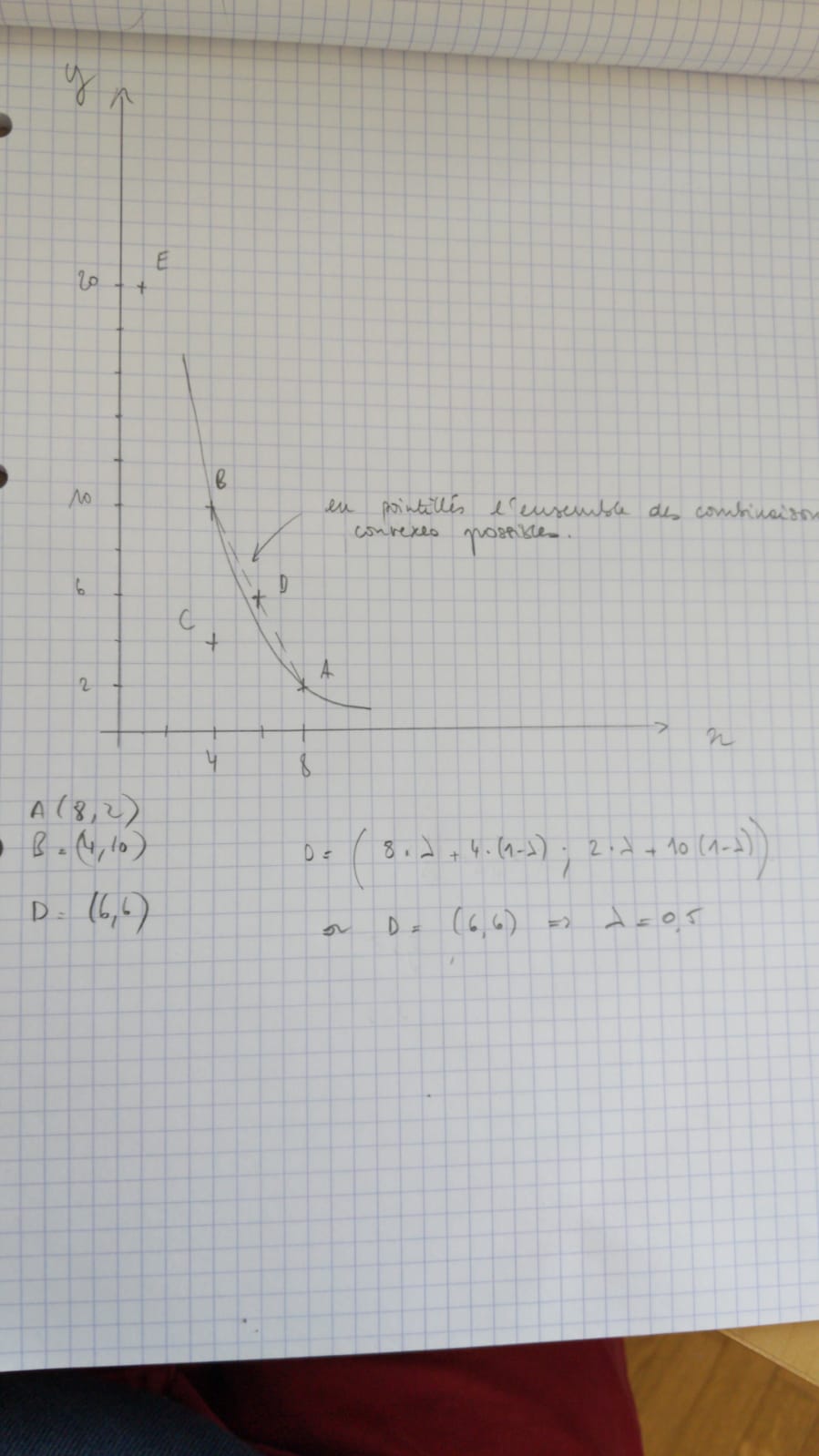
> réponse c est correct car D représente une combinaison convexe des paniers A et B !
Vous dites avoir pris un lambda = à 0.5 et c'est bien le bon lambda vous auriez du tomber sur D!
Mais attention, il y a une infinité de combinaisons convexes de A et B peut être trouvée en faisant varier lambda entre 0 et 1! cf graphique ci dessous.
D’accord ! Merci beaucoup !